Two weeks ago I spotted something on xbay, a 8569A spectrum analyzer, for parts or repair (“powers up, no display”), at a very reasonable price – just a bit above USD 300. This is not much more than the parts value of the 70 dB attenuator of this unit, so, a great deal in any case. The pictures shows a really beaten-up unit, black dirt all over it (mould?), and corrosion. At least the connectors seemed to have caps on them, fair enough. And it has option 1, a 100 MHz comb generator, good out to 20 GHz.
Unit as offered… doesn’t look very appealing.

Good news: I have a severely damaged 8565A here (broken frame, but still full of good parts), as a donor unit – looks like it is a unit that had been buried under tons of heavy stuff, or had a truck driving over it, a heavy truck. And, it doesn’t have a CRT.

The 8565A, 8569A and 8569B analyzers – these have a really easy to use design, three-knob operation, and are the best analyzers, from my point of view, for any general service and adjustment work, at any frequency above a few MHz. With resolution bandwidth down to 100 Hz, also up for some more special tasks. Sure, there are the 8568 and 8566 units (I also own a 8568B), but these are bulky, and you always need to push buttons AND turn knobs – more like for a cal lab or really high precision characterization work.
Plenty more modern analyzers exist, with LCD display, and all kinds of software features. They come at a price, and once you have experienced the responsiveness and easy of operation of the 8569 series, fancy LCD screens and color buttons can’t really be the reason to consider anything else. Good units, fully functional-refurbished, go for about USD 2-3k.
For general-purpose, low budget work – if you are looking for a 20+ GHz analyzer, there isn’t much that goes for less than 10k used, or 30-50k new. Some of the later, semi-portable 856x series might be an alternative. However, these have a rather small screen, just about 3.8″ diagonal, for the spectrum display, while the 8569B has 5.5″, and an electrostatic CRT, of excellent brilliance.
Also, keep in mind that the down-converted output can be easily converted to digital data by SDR, to recover even the most complex modulation schemes. No need to pay extra dollars to get custom plugins for modern analyzers. Such things pay off for the big corporations, but if you are up for special tasks, there is no way around dealing with some software, anyway.
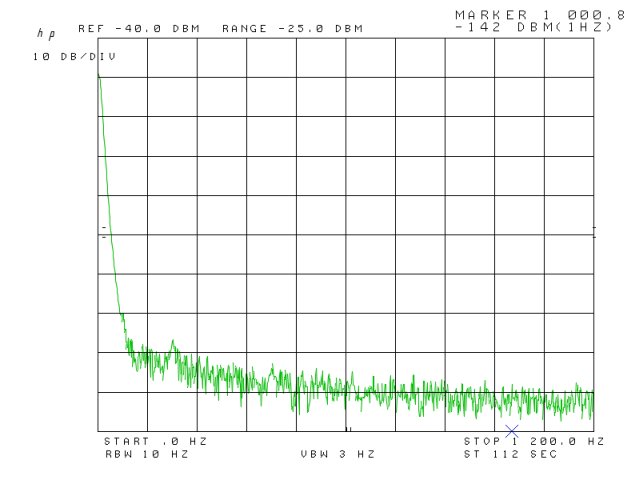
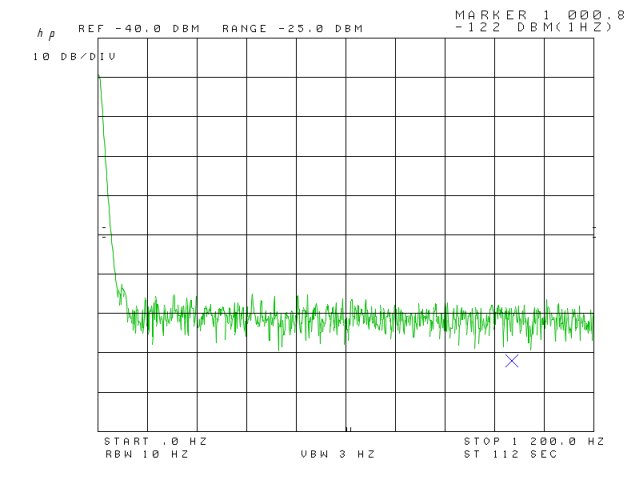
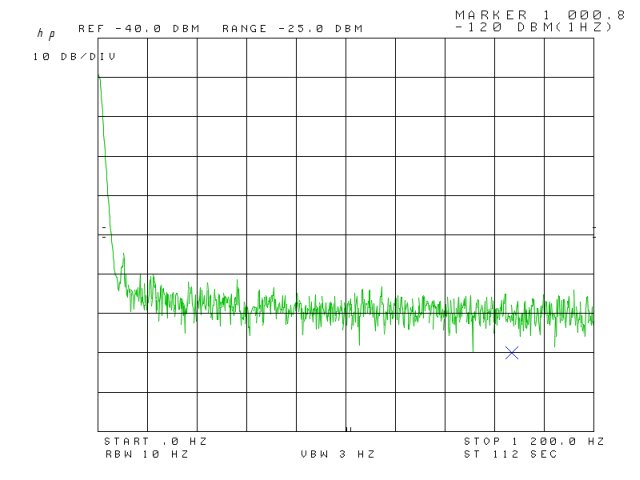
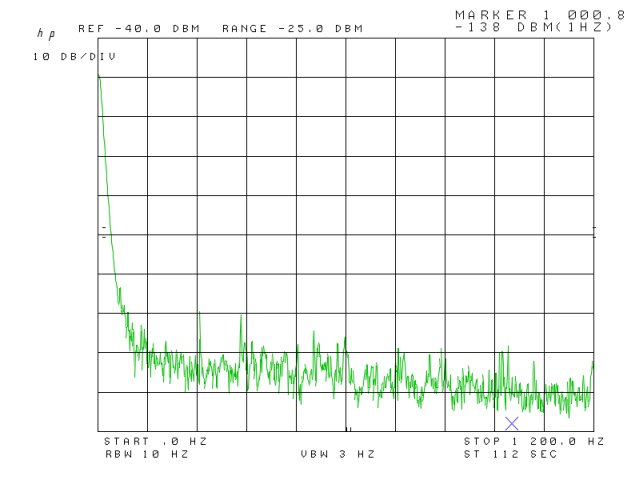
Currently, I use a 8569B in the workshop back in Germany, and here, in the US, I rely on a 8565A – which is essentially the same RF hardware, but has an analog storage display (variable persistence), rather than a digital display, like the 8659B. Also, the 8565A doesn’t have GPIB or other means of data bus, all computer-controlled measurments require the use of a A/D D/A converter unit.
So, it would be good to get the 8569A working, and eventually, sell-off the 8565A.
Historically, it seems the 8565A first appeared in about 1978. Looking up in some old HP catalogs – the 8569A appeared first in the 1982 edition (marked as “new”); quite surprising, because the unit I have here has a much earlier serial (1980) – and also the parts data back to end of 1980.

No doubt, seems to be a rather early unit (take the first two digits of the serial, and add 1960 = year of manufacture).
HP-Cat-1982-8569a
HP-Cat-1983-8569b
In the 1983 edition, HP already has the 8569B, with virtually identical specs. Quite interestingly, the 8565A (with the analog storage display!) remained available, in parallel with the digital-display 8569B, for many years – up until 1988 (at USD 34k, including option 1). The price difference was rather small, just about 10% (about USD 3k) more for the 8569B, with the much better display, and digital/automated control capabilities.
If you study the inner workings of the 856x in detail, it is also evident that a good part of the circuits were taken from 8555A analyzer, introduced in about 1970….
After all this, the analyzer arrived – well packaged. And first downside of it, it is 30 kg, 65 pounds, plus packaging. But hey, who needs to carry spectrum analyzers of this kind around – it will rest on the microwave test bench, along with generators, counters and so on, some 100s of pounds anyway.
Well, plugged it in – the display is really dead, but the frequency display is on. Powder supply is good. And, the X-Y output – when connected to a scope – you can actually get some signals, and it is sweeping. There is hope.
After some probing and basic tests, these are the items found so far:
(1) No display. However, there is a display signal on the deflection plates, and it is looking sound, so the digital display generator seems to work just fine. Just the CRT isn’t. Might be hard to fix, if the CRT is at fault – I can’t see the cathode glowing….
(2) The attenuator at 60-70 dB, and “0 dB” attenuator light at the front panel – not working (missing 20 dB attenuation; light off even when attenuation is set to 0 dB.
(3) Mechanical defect of the span knob – general mechanical soundness of the front panel. Will need very through cleaning, aligment, etc.
(4) Something is wrong with the tuning stabilizer, engaged at below 100 kHz span – when it is activated, it sets the span to zero, and never comes back, unless the stabilizer is de-activated.